已知点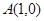 ,
, 、
、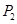 、
、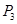 是平面直角坐标系上的三点,且
是平面直角坐标系上的三点,且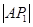 、
、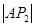 、
、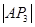 成等差数列,公差为
成等差数列,公差为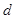 ,
,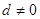 .
.
(1)若 坐标为
坐标为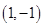 ,
,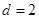 ,点
,点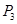 在直线
在直线 上时,求点
上时,求点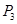 的坐标;
的坐标;
(2)已知圆 的方程是
的方程是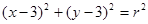
 ,过点
,过点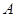 的直线交圆于
的直线交圆于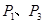 两点,
两点,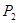 是圆
是圆 上另外一点,求实数
上另外一点,求实数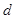 的取值范围;
的取值范围;
(3)若 、
、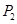 、
、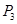 都在抛物线
都在抛物线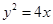 上,点
上,点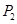 的横坐标为
的横坐标为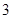 ,求证:线段
,求证:线段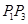 的垂直平分线与
的垂直平分线与 轴的交点为一定点,并求该定点的坐标.
轴的交点为一定点,并求该定点的坐标.
相关知识点
推荐套卷
已知点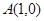 ,
, 、
、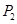 、
、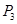 是平面直角坐标系上的三点,且
是平面直角坐标系上的三点,且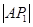 、
、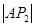 、
、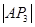 成等差数列,公差为
成等差数列,公差为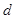 ,
,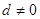 .
.
(1)若 坐标为
坐标为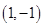 ,
,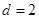 ,点
,点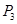 在直线
在直线 上时,求点
上时,求点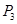 的坐标;
的坐标;
(2)已知圆 的方程是
的方程是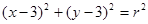
 ,过点
,过点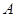 的直线交圆于
的直线交圆于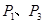 两点,
两点,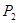 是圆
是圆 上另外一点,求实数
上另外一点,求实数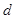 的取值范围;
的取值范围;
(3)若 、
、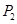 、
、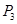 都在抛物线
都在抛物线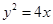 上,点
上,点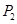 的横坐标为
的横坐标为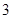 ,求证:线段
,求证:线段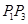 的垂直平分线与
的垂直平分线与 轴的交点为一定点,并求该定点的坐标.
轴的交点为一定点,并求该定点的坐标.