位于A处的雷达观测站,发现其北偏东45°,与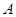 相距20
相距20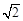 海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东
海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东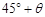
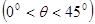 的C处,
的C处,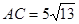 .在离观测站A的正南方某处E,
.在离观测站A的正南方某处E,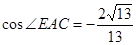
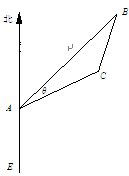
(1)求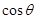 ; (2)求该船的行驶速度v(海里/小时);
; (2)求该船的行驶速度v(海里/小时);
相关知识点
推荐套卷
位于A处的雷达观测站,发现其北偏东45°,与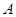 相距20
相距20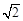 海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东
海里的B处有一货船正以匀速直线 行驶,20分钟后又测得该船只位于观测站A北偏东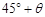
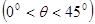 的C处,
的C处,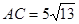 .在离观测站A的正南方某处E,
.在离观测站A的正南方某处E,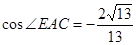

(1)求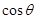 ; (2)求该船的行驶速度v(海里/小时);
; (2)求该船的行驶速度v(海里/小时);