如图,已知椭圆C: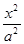 +
+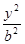 =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F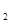 ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF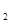 ⊥F
⊥F F
F ,O是坐标原点,OB垂直AF
,O是坐标原点,OB垂直AF 于B,且OF
于B,且OF =3OB.
=3OB.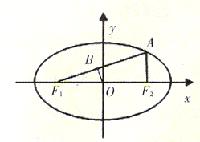
(Ⅰ)求椭圆C的离心率;
(Ⅱ)求t∈(0,b),使得命题“设圆x +y
+y =t
=t 上任意点M(x
上任意点M(x ,y
,y )处的切线交椭圆C于Q
)处的切线交椭圆C于Q 、Q
、Q 两点,那么OQ
两点,那么OQ ⊥OQ
⊥OQ ”成立.
”成立.
推荐套卷
如图,已知椭圆C: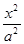 +
+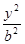 =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F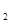 ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF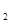 ⊥F
⊥F F
F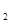 ,O是坐标原点,OB垂直AF
,O是坐标原点,OB垂直AF 于B,且OF
于B,且OF =3OB.
=3OB.
(Ⅰ)求椭圆C的离心率;
(Ⅱ)求t∈(0,b),使得命题“设圆x +y
+y =t
=t 上任意点M(x
上任意点M(x ,y
,y )处的切线交椭圆C于Q
)处的切线交椭圆C于Q 、Q
、Q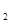 两点,那么OQ
两点,那么OQ ⊥OQ
⊥OQ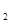 ”成立.
”成立.