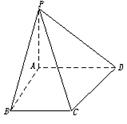
如图,在梯形ABCD中,AD∥BC,∠ABC=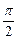 ,AB=
,AB= 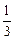 AD=a,
AD=a,
∠ADC=arccos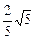 ,PA⊥面ABCD且PA=a.
,PA⊥面ABCD且PA=a.
(1)求异面直线AD与PC间的距离;
(2)在线段AD上是否存在一点F,使点A到平面PCF的距离为
相关知识点
推荐套卷
如图,在梯形ABCD中,AD∥BC,∠ABC=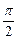 ,AB=
,AB= 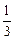 AD=a,
AD=a,
∠ADC=arccos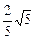 ,PA⊥面ABCD且PA=a.
,PA⊥面ABCD且PA=a.
(1)求异面直线AD与PC间的距离;
(2)在线段AD上是否存在一点F,使点A到平面PCF的距离为
