已知圆C的半径为1,圆心C在直线l1: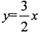
上，且其横坐标为整数，又圆C截直线
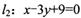所得的弦长为
•
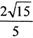(I )求圆C的标准方程;
(II)设动点P在直线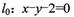
上，过点P作圆的两条切线PA, PB,切点分别为A ,B求四边形PACB面积的最小值.
相关试题
若
,且
成等比数列，求
中，内角
、
、
所对的边分别是
、
、
，已知
，
，
，求
，△
，试求函数
的最大值.
的前
项和为
，
（
）．
是等比数列，求出数列
，求数列
的前
；相关知识点
推荐套卷
已知圆C的半径为1,圆心C在直线l1: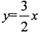上，且其横坐标为整数，又圆C截直线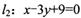所得的弦长为•
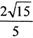(I )求圆C的标准方程;
(II)设动点P在直线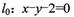上，过点P作圆的两条切线PA, PB,切点分别为A ,B求四边形PACB面积的最小值.
粤公网安备 44130202000953号