某校从参加考试的学生中抽出60名学生，将其成绩（均为整数）分成六组[40，50），[50，60） ．．．[90，100]后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：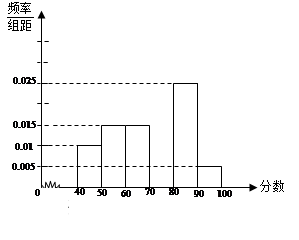
（1）求成绩落在[70，80）上的频率，并补全这个频率分布直方图；
（2）估计这次考试的及格率（60分及以上为及格）和平均分；
为非零向量，且
，求
与
的夹角
。
和点
，其中
，若
,求
得值。
，计算
的值
，且
为第三象限角，求
及
的值。
的不等式
．
时，求此不等式的解集；
，求实数
的取值范围．相关知识点
推荐套卷
某校从参加考试的学生中抽出60名学生，将其成绩（均为整数）分成六组[40，50），[50，60） ．．．[90，100]后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：
（1）求成绩落在[70，80）上的频率，并补全这个频率分布直方图；
（2）估计这次考试的及格率（60分及以上为及格）和平均分；
粤公网安备 44130202000953号