)为了了解中学生的身高情况,对某校中学生同年龄的若干名女生的身高进行了测量,将所得数据整理后,画出频率分布直方图(如图),已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6(单位:cm)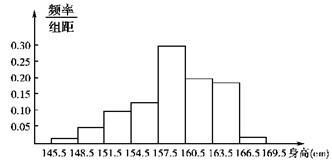
(1)参加这次测试的学生人数是多少?
(2)身高在哪个范围内的学生人数最多?这一范围内的人数是多少?
(3)如果本次测试身高在154.5 cm以上的为良好,试估计该校学生身高良好率是多少?
相关知识点
推荐套卷
 ,其中3<x<6,a 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
,其中3<x<6,a 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。 的对称轴为坐标轴,焦点是(0,
的对称轴为坐标轴,焦点是(0, ),(0,
),(0,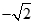 ),又点
),又点
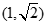 在椭圆
在椭圆 的斜率为
的斜率为 、
、 两点,求
两点,求 面积的最大值.
面积的最大值. x3-
x3-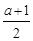 x2+a x.
x2+a x.
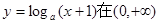 内单调递减;
内单调递减;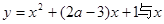 轴交于不同的两点.
轴交于不同的两点. 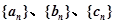 满足
满足
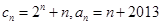 ,当
,当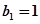 时,求数列
时,求数列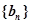 的通项公式.
的通项公式.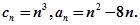 求正整数
求正整数 使得一切
使得一切 均有
均有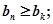
 粤公网安备 44130202000953号
粤公网安备 44130202000953号