某校七年级共有500名学生，团委准备调查他们对“低碳”知识的了解程度．
（1）在确定调查方式时，团委设计了以下三种方案：
方案一：调查七年级部分女生；
方案二：调查七年级部分男生；
方案三：到七年级每个班去随机调查一定数量的学生．
请问其中最具有代表性的一个方案是______________；
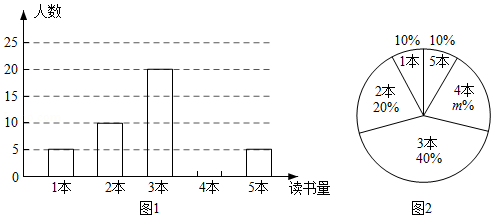
（2）团委采用了最具有代表性的调查方案，并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示)请你根据图中信息，将其补充完整；
（3）请你估计该校七年级约有多少名学生比较了解“低碳”知识．
相关试题
，求
的算术平方根．
（1）小明说：“请你任意想一个数，把这个数乘2后加8，然后除以4，再减去你原来所想的那个数的
，我可以知道你计算的结果是2．”
请你帮助小明说明上述结论的正确性．
如果设任意想的那个数为x，则根据题意，得代数式（请完善下面的解题过程）：
（2）在（1）中，得到的代数式化简后结果为2，它不含有x，我们称之为“与x无关”．
试解决下列“无关”类问题：
①多项式
的值（）
| A．仅与x的大小无关 | B．仅与y的大小无关 |
| C．与x、y的大小都无关 | D．与x、y的大小都有关 |
②如果已知代数式
的值与其中某个字母的取值无关，你能求出哪一个字母的值？此时这个字母的值是多少？
张（
）相关知识点
推荐套卷
粤公网安备 44130202000953号