(本小题满分12分)某市电信宽带网用户收费标准如下表:(假定每月初均可以和电信部门约定上网方案)
方案
|
类别
|
基本费用
|
超时费用
|
甲
|
包月制
|
70元
|
|
乙
|
有限包月制(限60小时)
|
50元
|
0.05元/分钟(无上限)
|
丙
|
有限包月制(限30小时)
|
30元
|
0.05元/分钟(无上限)
|
(1)若某用户某月上网时间为T小时,当T在什么范围内时,选择甲方案最合算?并说明理由
(2)王先生因工作需要需在家上网,他一年内每月的上网时间T(小时)与月份n的函数关系为T = f (n) =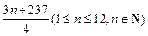 .若公司能报销王先生全年的上网费用,问公司最少会为此花多少元?
.若公司能报销王先生全年的上网费用,问公司最少会为此花多少元?