本小题满分10分）选修4—4：坐标系与参数方程.
已知曲线C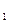
：
（
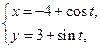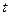为参数）， C
：
（
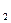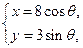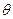为参数）。
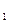（1）化C，C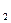的方程为普通方程，并说明它们分别表示什么曲线；
（2）若C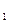上的点P对应的参数为
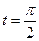，Q为C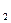上的动点，求
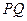中点
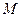到直线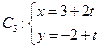
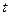，（为参数）距离的最小值.
相关试题
,求P点的坐标；
,试 用
表示
.
是
所在平面内一点,
的中点为
,
的中点为
,
的中点为
.证明:只有唯一的一点
，AD与BC交于点M，设
=
，
=
，用
.
，推荐套卷
本小题满分10分）选修4—4：坐标系与参数方程.
已知曲线C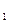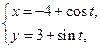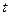： （为参数）， C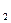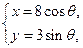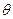：（为参数）。
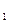（1）化C，C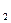的方程为普通方程，并说明它们分别表示什么曲线；
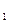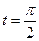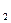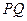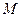（2）若C上的点P对应的参数为，Q为C上的动点，求中点到直线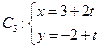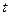，（为参数）距离的最小值.
粤公网安备 44130202000953号