如图,在平面直角坐标系中,已知抛物线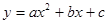 交
交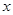 轴于
轴于 两点,交
两点,交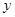 轴于点
轴于点 .
.
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交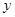 轴于点E、F两点,求劣弧
轴于点E、F两点,求劣弧  的长;
的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于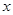 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
相关知识点
推荐套卷
如图,在平面直角坐标系中,已知抛物线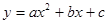 交
交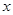 轴于
轴于 两点,交
两点,交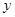 轴于点
轴于点 .
.
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交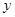 轴于点E、F两点,求劣弧
轴于点E、F两点,求劣弧  的长;
的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于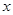 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.