设各项均为正实数的数列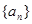 的前
的前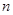 项和为
项和为 ,且满足
,且满足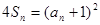 (
(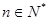 ).
).
(Ⅰ)求数列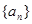 的通项公式;
的通项公式;
(Ⅱ)设数列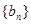 的通项公式为
的通项公式为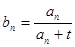 (
(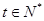 ),若
),若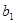 ,
, ,
,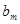 (
(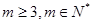 )成等差数列,求
)成等差数列,求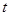 和
和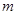 的值;
的值;
(Ⅲ)证明:存在无穷多个三边成等比数列且互不相似的三角形,其三边长为数列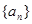 中的三项
中的三项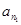 ,
,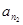 ,
,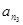 .
.
推荐套卷
设各项均为正实数的数列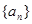 的前
的前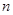 项和为
项和为 ,且满足
,且满足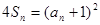 (
(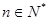 ).
).
(Ⅰ)求数列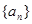 的通项公式;
的通项公式;
(Ⅱ)设数列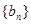 的通项公式为
的通项公式为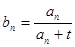 (
(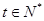 ),若
),若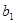 ,
, ,
,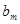 (
(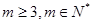 )成等差数列,求
)成等差数列,求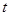 和
和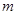 的值;
的值;
(Ⅲ)证明:存在无穷多个三边成等比数列且互不相似的三角形,其三边长为数列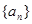 中的三项
中的三项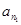 ,
,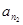 ,
,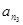 .
.