某饮料厂为了开发新产品,用 种果汁原料和
种果汁原料和 种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制
种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制 千克,两种饮料的成本总额为
千克,两种饮料的成本总额为 元.
元.
(1)已知甲种饮料成本每千克4元,乙种饮料成本每千克3元,请你写出 与
与 之间的函数关系式;
之间的函数关系式;
(2)若用19千克 种果汁原料和17.2千克
种果汁原料和17.2千克 种果汁原料试制甲、乙两种新型饮料,右表是试验的相关数据;请你列出关于
种果汁原料试制甲、乙两种新型饮料,右表是试验的相关数据;请你列出关于 且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使
且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使 值最小,最小值是多少?
值最小,最小值是多少?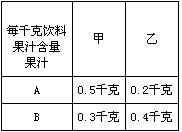
相关知识点
推荐套卷
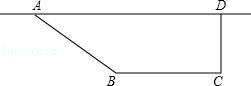


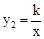 (k≠0)的图象相交于A、B两点,点A的纵坐标为2.
(k≠0)的图象相交于A、B两点,点A的纵坐标为2.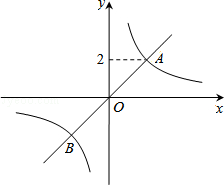
 粤公网安备 44130202000953号
粤公网安备 44130202000953号