菱形ABCD的边长为2,∠BAD=60°,对角线AC,BD相交于点O,动点P在线段AC上从点A向点C运动,过P作PE∥AD,交AB于点E,过P作PF∥AB,交AD于点F,四边形QHCK与四边形PEAF关于直线BD对称.设菱形ABCD被这两个四边形盖住部分的面积为S,AP=x:则:
(1)对角线AC的长为 ;S菱形ABCD= ;
(2)用含x的代数式表示S;
(3)设点P在移动过程中所得两个四边形PEAF与QHCK的重叠部分面积为y,当y=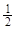 S菱形ABCD时,求x的值.
S菱形ABCD时,求x的值.
相关知识点
推荐套卷
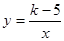 (k为常数,且k≠5)经过点A(1,3).
(k为常数,且k≠5)经过点A(1,3).
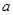 =,
=,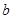 =;
=;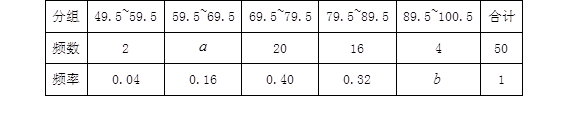
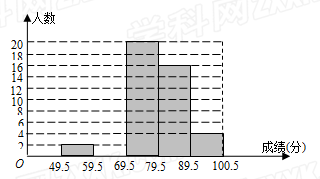
 ,其中
,其中 .
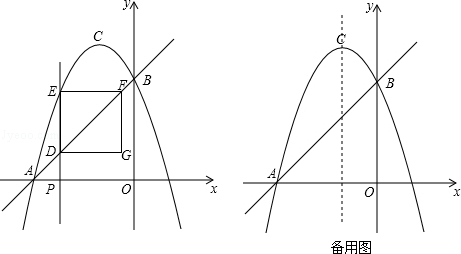
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号