计算:
(1)(-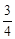 )×(-1
)×(-1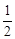 )÷(-1
)÷(-1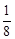 )
)
(2)-22–23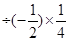 +(-1)2+
+(-1)2+
(3)先化简,再求值: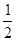 (8a2-6a)-(2a2+a-1)+2(1-
(8a2-6a)-(2a2+a-1)+2(1-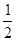 a2+2a),其中a=2.
a2+2a),其中a=2.
相关知识点
推荐套卷
计算:
(1)(-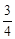 )×(-1
)×(-1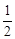 )÷(-1
)÷(-1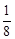 )
)
(2)-22–23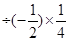 +(-1)2+
+(-1)2+
(3)先化简,再求值: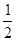 (8a2-6a)-(2a2+a-1)+2(1-
(8a2-6a)-(2a2+a-1)+2(1-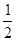 a2+2a),其中a=2.
a2+2a),其中a=2.