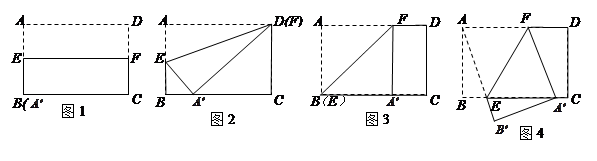矩形ABCD中,AD=5,AB=3,将矩形ABCD沿某直线折叠,使点A的对应点A′落在线段BC上,再打开得到折痕EF.
(1)当A′与B重合时(如图1),EF= ;当折痕EF过点D时(如图2),求线段EF的长;
(2)观察图3和图4,设BA′=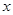 ,①当
,①当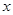 的取值范围是 时,四边形AEA′F是菱形;②在①的条件下,利用图4证明四边形AEA′F是菱形.
的取值范围是 时,四边形AEA′F是菱形;②在①的条件下,利用图4证明四边形AEA′F是菱形.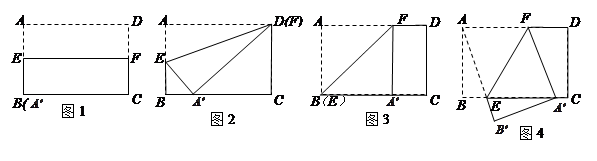
相关知识点
推荐套卷
矩形ABCD中,AD=5,AB=3,将矩形ABCD沿某直线折叠,使点A的对应点A′落在线段BC上,再打开得到折痕EF.
(1)当A′与B重合时(如图1),EF= ;当折痕EF过点D时(如图2),求线段EF的长;
(2)观察图3和图4,设BA′=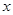 ,①当
,①当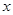 的取值范围是 时,四边形AEA′F是菱形;②在①的条件下,利用图4证明四边形AEA′F是菱形.
的取值范围是 时,四边形AEA′F是菱形;②在①的条件下,利用图4证明四边形AEA′F是菱形.