如图1，在矩形ABCD中，AB=6cm，BC=12cm，点P从点A开始以1cm/s的速度沿AB边向点B运动，点Q从点B以2cm/s的速度沿BC边向点C运动，如果P、Q同时出发，设运动时间为ts，
（1）当t=2时，求△PBQ的面积；
（2）当t=
时，试说明△DPQ是直角三角形；
（3）当运动3s时，P点停止运动，Q点以原速立即向B点返回，在返回的过程中，DP是否能平分∠ADQ？若能，求出点Q运动的时间；若不能，请说明理由．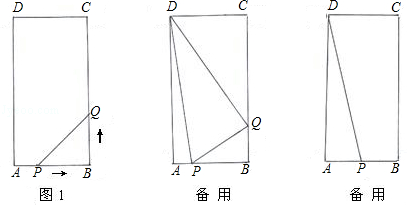
相关知识点
推荐套卷
如图1，在矩形ABCD中，AB=6cm，BC=12cm，点P从点A开始以1cm/s的速度沿AB边向点B运动，点Q从点B以2cm/s的速度沿BC边向点C运动，如果P、Q同时出发，设运动时间为ts，
（1）当t=2时，求△PBQ的面积；
（2）当t=时，试说明△DPQ是直角三角形；
（3）当运动3s时，P点停止运动，Q点以原速立即向B点返回，在返回的过程中，DP是否能平分∠ADQ？若能，求出点Q运动的时间；若不能，请说明理由．
粤公网安备 44130202000953号