某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品在该售价的基础上每上涨1元，则每个月少卖10件（每件售价不能高于65元）．设每件商品的售价上涨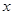
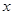元（为正整数），每个月的销售利润为
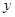元．(14分)
（1）求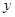与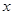的函数关系式并直接写出自变量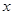的取值范围；
（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？
,求
的值.
，且
．
、
的值；
、
、
的值．
，求（1）
；
的值．
．推荐套卷
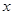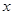某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品在该售价的基础上每上涨1元，则每个月少卖10件（每件售价不能高于65元）．设每件商品的售价上涨元（为正整数），每个月的销售利润为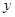元．(14分)
（1）求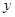与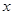的函数关系式并直接写出自变量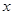的取值范围；
（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？
粤公网安备 44130202000953号