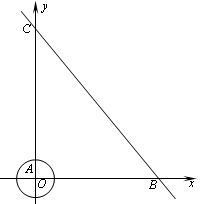
如图,在直角坐标系中,半径为1的⊙A圆心与原点O重合,直线l分别交x轴、y轴于点B、C,若点B的坐标为(6,0),tan∠ABC=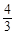 .
.
(1)若点P是⊙A上的动点,求P到直线BC的最小距离,并求此时点P的坐标;
(2)若点A从原点O出发,以1个单位/秒的速度沿着线路OB→BC→CO运动,回到点O停止运动,⊙A随着点A的运动而移动.设点A运动的时间为t.
①求⊙A在整个运动过程中与坐标轴相切时t的取值;
②求⊙A在整个运动过程中所扫过的图形的面积为 .
相关知识点
推荐套卷

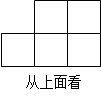
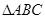 中
中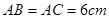 ,
,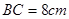 .点
.点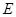 是线段
是线段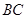 边上的一动点(不含
边上的一动点(不含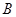 、
、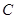 两端点),连结
两端点),连结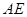 ,作
,作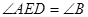 ,交线段
,交线段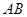 于点
于点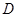 .
. 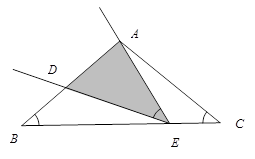
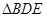 ∽
∽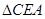 ;
;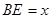 ,
,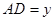 ,请写
,请写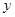 与
与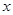 之间的函数关系式,并求
之间的函数关系式,并求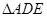 能否构成等腰三角形?若能,求出
能否构成等腰三角形?若能,求出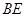 的长;若不能,请说明理由。
的长;若不能,请说明理由。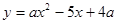 与
与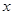 轴相交于点
轴相交于点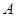 、
、 ,且经过点
,且经过点 (5,4).该抛物线顶点为
(5,4).该抛物线顶点为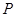 .
.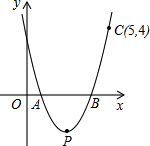
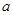 的值和该抛物线顶点
的值和该抛物线顶点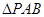 的面积;
的面积;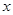 吨,那么这个月该单元居民只交10元水费.如果超过
吨,那么这个月该单元居民只交10元水费.如果超过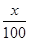 元交费.
元交费. 粤公网安备 44130202000953号
粤公网安备 44130202000953号