世博会在我国的上海举行,在网上随机调取了5月份中的某10天持票入园参观的人数,绘成下面的统计图.根据图中的信息回答下列问题:
(1)求出这10天持票入园人数的平均数、中位数和众数;
(2)不考虑其它因素的影响,以这10天的数据作为样本,估计在世博会开馆的184天中,持票入园人数超过30万人的有多少天?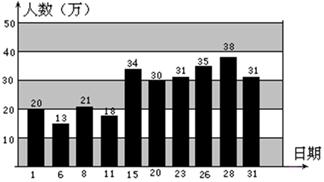
相关知识点
推荐套卷
世博会在我国的上海举行,在网上随机调取了5月份中的某10天持票入园参观的人数,绘成下面的统计图.根据图中的信息回答下列问题:
(1)求出这10天持票入园人数的平均数、中位数和众数;
(2)不考虑其它因素的影响,以这10天的数据作为样本,估计在世博会开馆的184天中,持票入园人数超过30万人的有多少天?