已知直线y=kx-3与x轴交于点A(4,0),与y轴交于点C,抛物线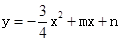 经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.
经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.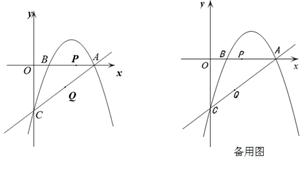
(1)求此抛物线的解析式和直线的解析式;
(2)如果点P和点Q同时出发,运动时间为t(秒),试问当t为何值时,以A、P、Q为顶点的三角形与△AOC相似;
(3)在直线CA上方的抛物线上是否存在一点D,使得△ACD的面积最大.若存在,求出点D的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
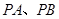 分别与
分别与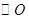 相切于点
相切于点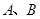 ,点
,点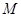 在
在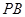 上,且
上,且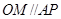 ,
,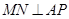 ,垂足为
,垂足为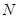 .
.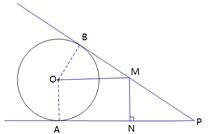
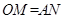 ;
; ,
,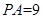 ,求
,求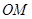 的长
的长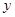 (克/立方米)与海拔高度
(克/立方米)与海拔高度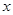 (米)之间近似地满足一次函数关系.经测量,在海拔高度为0米的地方,空气含氧量约为299克/立方米;在海拔高度为2000米的地方,空气含氧量约为235克/立方米.
(米)之间近似地满足一次函数关系.经测量,在海拔高度为0米的地方,空气含氧量约为299克/立方米;在海拔高度为2000米的地方,空气含氧量约为235克/立方米.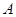 处测得湖心岛上的迎宾槐
处测得湖心岛上的迎宾槐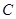 处位于北偏东
处位于北偏东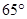 方向,然后,他从凉亭
方向,然后,他从凉亭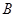 处,测得湖心岛上的迎宾槐
处,测得湖心岛上的迎宾槐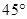 方向(点
方向(点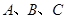 在同一水平面上).请你利用小明测得的相关数据,求湖心岛上的迎宾槐
在同一水平面上).请你利用小明测得的相关数据,求湖心岛上的迎宾槐 ,
, )
)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号