甲、乙两车同时同时出发从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍.两车距离A地的路程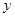 (千米)与行驶时间
(千米)与行驶时间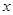 (时)的函数图象如图所示.
(时)的函数图象如图所示.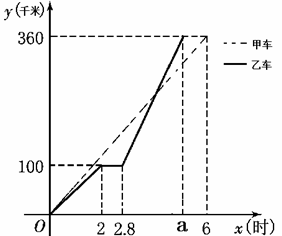
(1)求甲车距离A地的路程 (千米)与行驶时间
(千米)与行驶时间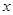 (时)之间的函数关系式;
(时)之间的函数关系式;
(2)当x=2.8时,甲、乙两车之间的距离是 千米;乙车到达B地所用的时间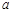 的值为 ;
的值为 ;
(3)行驶过程中,两车出发多长时间首次后相遇?
相关知识点
推荐套卷
甲、乙两车同时同时出发从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍.两车距离A地的路程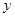 (千米)与行驶时间
(千米)与行驶时间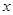 (时)的函数图象如图所示.
(时)的函数图象如图所示.
(1)求甲车距离A地的路程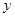 (千米)与行驶时间
(千米)与行驶时间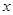 (时)之间的函数关系式;
(时)之间的函数关系式;
(2)当x=2.8时,甲、乙两车之间的距离是 千米;乙车到达B地所用的时间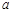 的值为 ;
的值为 ;
(3)行驶过程中,两车出发多长时间首次后相遇?