已知向量m=(cos ,1),n=(
,1),n=(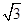 sin
sin ,cos2
,cos2 ).
).
(1)若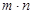 =1,求
=1,求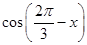 的值;
的值;
(2)记f(x)=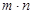 ,在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
,在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
推荐套卷
已知向量m=(cos ,1),n=(
,1),n=(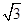 sin
sin ,cos2
,cos2 ).
).
(1)若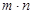 =1,求
=1,求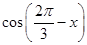 的值;
的值;
(2)记f(x)=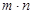 ,在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
,在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.