如图,在半径为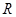 、圆心角为
、圆心角为 的扇形金属材料中剪出一个长方形
的扇形金属材料中剪出一个长方形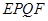 ,并且
,并且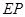 与
与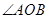 的平分线
的平分线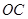 平行,设
平行,设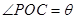 .
.
(1)试写出用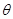 表示长方形
表示长方形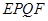 的面积
的面积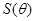 的函数;
的函数;
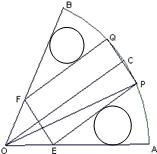
(2)在余下的边角料中在剪出两个圆(如图所示),试问当矩形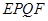 的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.
的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.
相关知识点
推荐套卷
如图,在半径为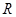 、圆心角为
、圆心角为 的扇形金属材料中剪出一个长方形
的扇形金属材料中剪出一个长方形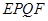 ,并且
,并且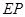 与
与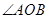 的平分线
的平分线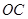 平行,设
平行,设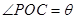 .
.
(1)试写出用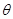 表示长方形
表示长方形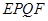 的面积
的面积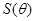 的函数;
的函数;
(2)在余下的边角料中在剪出两个圆(如图所示),试问当矩形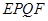 的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.
的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.