（本小题满分12分）
已知函数f(x)="lnx-ax-3" (a≠0).
（1）讨论函数f(x)的单调性；
（2）若对于任意的a∈[1,2]，函数g(x)=x3+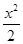
[m-2f′(x)]在区间(a,3)上有最值，求实数m的取值范围
，
的最小值为
，求
的值
图像是否为中心对称图形
=
（
）定义域为
，若所有点（
）（
）构成一正方形，求
的值
，
在函数
的图像上，称
为函数
的一组关于原点的中心对称点，
关于原点的中心对称点有多少组
=
（
的对称中心为
推荐套卷
（本小题满分12分）
已知函数f(x)="lnx-ax-3" (a≠0).
（1）讨论函数f(x)的单调性；
（2）若对于任意的a∈[1,2]，函数g(x)=x3+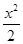 [m-2f′(x)]在区间(a,3)上有最值，求实数m的取值范围
粤公网安备 44130202000953号