已知方程tan2x一
tan x+1=0在x
[0，n
)( nN*)内所有根的和记为an
(1)写出an的表达式；(不要求严格的证明)
(2)记Sn = a1 + a2 +…+ an求Sn；
(3)设bn =(kn一5) ，若对任何nN* 都有an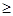
bn，求实数k的取值范围．
相关试题
满足： 
；
时，求
与
的关系式，并求数列
的模均为1，它们相互之间的夹角均为
。
；
，求
的取值范围。
，函数
，
时，
,求常数
，
的值.
是奇函数. 
的值；
在区间
上单调递增，求实数
的取值范围.
：关于
的不等式
，对一切
恒成立，命题
：函数
是增函数，若
为真，
为假，求实数
的取值范围.推荐套卷
已知方程tan2x一tan x+1=0在x[0，n)( nN*)内所有根的和记为an
(1)写出an的表达式；(不要求严格的证明)
(2)记Sn = a1 + a2 +…+ an求Sn；
(3)设bn =(kn一5) ，若对任何nN* 都有an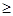bn，求实数k的取值范围．
粤公网安备 44130202000953号