设数列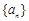 是有穷等差数列,给出下面数表:
是有穷等差数列,给出下面数表: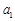

 ……
…… 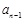
 第1行
第1行
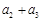 ……
……  第2行
第2行
… … …
… …
… 第n行
上表共有行,其中第1行的个数为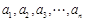 ,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为
,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为 .
.
(1)求证:数列 成等比数列;
成等比数列;
(2)若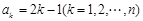 ,求和
,求和 .
.
相关知识点
推荐套卷
 ,其中向量
,其中向量 ,
,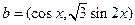 ,
,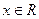 .
. ,且
,且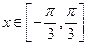 ,求x的值;
,求x的值; 的图像按向量
的图像按向量
 平移后得到函数
平移后得到函数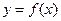 的图像,求实数
的图像,求实数 的值。
的值。 ,求实数λ的取值范围.
,求实数λ的取值范围. 的比为3∶2,求m的值.
的比为3∶2,求m的值. . 求点M 分
. 求点M 分 所成的比.
所成的比.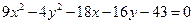 的图像C按向量
的图像C按向量 . 平移后得到的图像的方程为
. 平移后得到的图像的方程为 .试求向量
.试求向量 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号