已知椭圆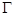 的方程为
的方程为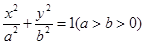 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b).
(1)若直角坐标平面上的点M、A(0,-b),B(a,0)满足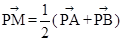 ,求点
,求点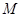 的坐标;
的坐标;
(2)设直线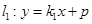 交椭圆
交椭圆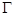 于
于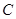 、
、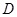 两点,交直线
两点,交直线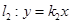 于点
于点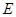 .若
.若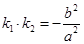 ,证明:
,证明: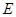 为
为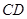 的中点;
的中点;
(3)对于椭圆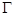 上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆
上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆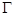 上存在不同的两个交点
上存在不同的两个交点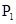 、
、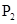 满足
满足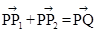 ,写出求作点
,写出求作点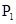 、
、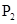 的步骤,并求出使
的步骤,并求出使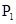 、
、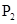 存在的θ的取值范围.
存在的θ的取值范围.
推荐套卷
已知椭圆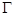 的方程为
的方程为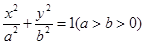 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b).
(1)若直角坐标平面上的点M、A(0,-b),B(a,0)满足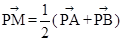 ,求点
,求点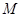 的坐标;
的坐标;
(2)设直线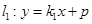 交椭圆
交椭圆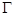 于
于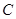 、
、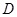 两点,交直线
两点,交直线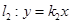 于点
于点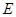 .若
.若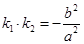 ,证明:
,证明: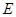 为
为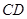 的中点;
的中点;
(3)对于椭圆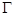 上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆
上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆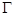 上存在不同的两个交点
上存在不同的两个交点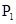 、
、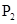 满足
满足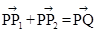 ,写出求作点
,写出求作点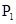 、
、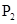 的步骤,并求出使
的步骤,并求出使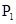 、
、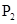 存在的θ的取值范围.
存在的θ的取值范围.