将抛物线c1：y=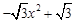
沿x轴翻折，得到抛物线c2，如图所示.
（1）请直接写出抛物线c2的表达式；
（2）现将抛物线c1向左平移m个单位长度，平移后得到的新抛物线的顶点为M，与x轴的交点从左到右依次为A，B；将抛物线c2向右也平移m个单位长度，平移后得到的新抛物线的顶点为N，与x轴的交点从左到右依次为D，E.
①用含m的代数式表示点A和点E的坐标；
②在平移过程中，是否存在以点A，M，E为顶点的三角形是直角三角形的情形？若存在，请求出此时m的值；若不存在，请说明理由.
相关试题
⑴半径为R的圆的面积恰好是半径为5与半径为2的两个圆面积之差，求R的值。
（2）某次商品交易会上，所有参加会议的商家之间都签订了一份合同，共签订合同36份，求共有多少商家参加了交易会？
； 
相关知识点
推荐套卷
粤公网安备 44130202000953号