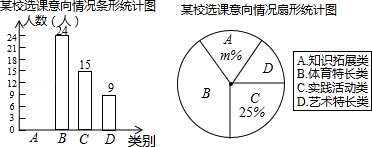
某校开展以“迎新年”为主题的艺术活动，举办了四个项目的比赛.它们分别是：A演讲、B唱歌、C书法、D绘画.要求每位同学必须参加且限报一项.以九(一)班为样本进行统计，并将统计结果绘制如下两幅统计图，请你结合图中所给出的信息解答下列问题：
(1)求出参加绘画比赛的学生人数占全班总人数的百分比；
(2)求出扇形统计图中参加书法比赛的学生所在的扇形圆心角的度数；
(3)若该校九年级学生共有500人，请你估计这次活动中参加演讲和唱歌的学生共有多少人？
相关试题
的两个实数根．
，且m为整数，求m的值．
其中，x=—3
中，
=90°，点
是弧
上的一个动点（不与点
、
重合）
，
，垂足分别为
、
．
时，求线段
的长；
中是否存在长度保持不变的边？如果存在，请指出并求其长度，如果不存在，请说明理由；
，
，求
的函数关系式，并写出相关知识点
推荐套卷
粤公网安备 44130202000953号