(本小题满分14分)
已知函数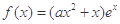 ,其中e是自然数的底数,
,其中e是自然数的底数, .
.
(1)当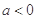 时,解不等式
时,解不等式 ;
;
(2)当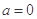 时,求正整数k的值,使方程
时,求正整数k的值,使方程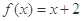 在[k,k+1]上有解;
在[k,k+1]上有解;
(3)若 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求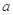 的取值范围.
的取值范围.
相关知识点
推荐套卷
(本小题满分14分)
已知函数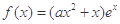 ,其中e是自然数的底数,
,其中e是自然数的底数, .
.
(1)当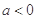 时,解不等式
时,解不等式 ;
;
(2)当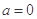 时,求正整数k的值,使方程
时,求正整数k的值,使方程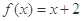 在[k,k+1]上有解;
在[k,k+1]上有解;
(3)若 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求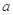 的取值范围.
的取值范围.