（本题8分））如图，点A，B，C，D在⊙O上，AB=AC，AD与BC相交于点E，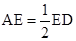
，延长DB到点F，使
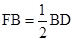，连接AF．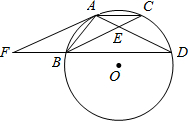
（1）证明：△BDE∽△FDA；
（2）试判断直线AF与⊙O的位置关系，并给出证明．
相关试题
，其中
的图象与反比例函数
的图象交于点
取何值时，反比例函数的值大于正比例函数的值？
是反比例函数图象上的一动点，其中
过点
作直线
轴，交
轴于点
；过点
作直线
轴交
，交直线
于点
．当四边形
的面积为6时，请判断线段
与
的大小关系，并说明理由．相关知识点
推荐套卷
（本题8分））如图，点A，B，C，D在⊙O上，AB=AC，AD与BC相交于点E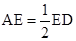，，延长DB到点F，使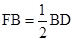，连接AF．
（1）证明：△BDE∽△FDA；
（2）试判断直线AF与⊙O的位置关系，并给出证明．
粤公网安备 44130202000953号