某游泳馆的游泳池长50米,甲、乙二人分别在游泳池相对的A、B两边同时向另一边游去,其中s表示与A边的距离,t表示游泳时间,如图,l1,l2分别表示甲、乙两人的s与t的关系.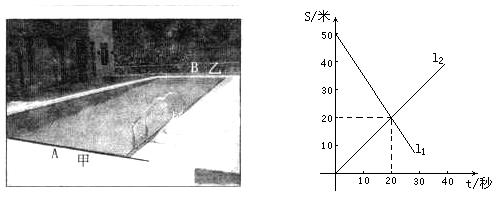
(1)l1表示谁到A边的距离s与游泳时间t的关系;
(2)甲、乙哪个速度快?
(3)游泳多长时间,两人相遇?
(4) t=30秒时,两人相距多少米?
相关知识点
推荐套卷
某游泳馆的游泳池长50米,甲、乙二人分别在游泳池相对的A、B两边同时向另一边游去,其中s表示与A边的距离,t表示游泳时间,如图,l1,l2分别表示甲、乙两人的s与t的关系.
(1)l1表示谁到A边的距离s与游泳时间t的关系;
(2)甲、乙哪个速度快?
(3)游泳多长时间,两人相遇?
(4) t=30秒时,两人相距多少米?