全面二孩政策于2016年1月1日正式实施,黔南州某中学对八年级部分学生进行了随机问卷调查,其中一个问题“你爸妈如果给你添一个弟弟(或妹妹),你的态度是什么?”共有如下四个选项(要求仅选择一个选项)
.非常愿意
.愿意
.不愿意
.无所谓
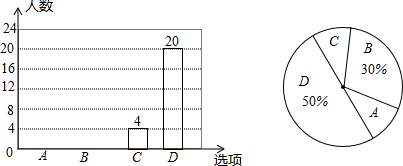
如图是根据调查结果绘制的两幅不完整的统计图,请结合图中信息解答以下问题:
(1)试问本次问卷调查一共调查了多少名学生?并补全条形统计图;
(2)若该年级共有450名学生,请你估计全年级可能有多少名学生支持(即态度为“非常愿意”和“愿意”
爸妈给自己添一个弟弟(或妹妹)?
(3)在年级活动课上,老师决定从本次调查回答“不愿意”的同学中随机选取2名同学来谈谈他们的想法,而本次调查回答“不愿意”的这些同学中只有一名男同学,请用画树状图或列表的方法求选取到两名同学中刚好有这位男同学的概率.