有两个可以自由转动的质地均匀转盘都被分成了3.个全等的扇形,在每一扇形内均标有不同的自然数,如图所示,转动转盘,两个转盘停止后观察并记录两个指针所指扇形内的数字(若指针停在扇形的边线上,当作指向上边的扇形).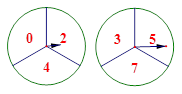
(l)用列表法或画树形图法求出同时转动两个转盘一次的所有可能结果;
(2)同时转动两个转盘一次,求“记录的两个数字之和为7”的概率.
相关知识点
推荐套卷
有两个可以自由转动的质地均匀转盘都被分成了3.个全等的扇形,在每一扇形内均标有不同的自然数,如图所示,转动转盘,两个转盘停止后观察并记录两个指针所指扇形内的数字(若指针停在扇形的边线上,当作指向上边的扇形).
(l)用列表法或画树形图法求出同时转动两个转盘一次的所有可能结果;
(2)同时转动两个转盘一次,求“记录的两个数字之和为7”的概率.