(本小题满分12分)
为了了解小学五年级学生的体能情况,抽取了实验小学五年级部分学生进行踢毽子测试,将所得的数据整理后画出频率分布直方图(如图),已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数是5.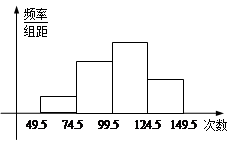
(Ⅰ)求第四小组的频率和参加这次测试的学生人数;
(Ⅱ)在这次测试中,问学生踢毽子次数的中位数落在第几小组内?
(Ⅲ)在这次跳绳测试中,规定跳绳次数在110以上的为优秀,试估计该校此年级跳绳成绩的优秀率是多少?
相关知识点
推荐套卷
 ,α∈(0,
,α∈(0, ),sin(β-
),sin(β- ,β∈(
,β∈(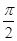 ).
).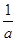 )(x+4)≤0的解集.
)(x+4)≤0的解集.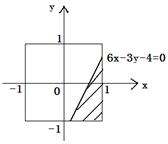
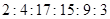 ,第二小组频数为12.
,第二小组频数为12.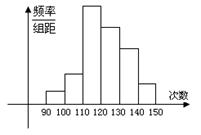
 粤公网安备 44130202000953号
粤公网安备 44130202000953号