本题满分分已知A，B，C，D，E，F是边长为1的正六边形的6个顶点，在顶点取自A，B，C，D，E，F的所有三角形中，随机(等可能)取一个三角形．设随机变量X为取出三角形的面积．
(Ⅰ) 求概率P ( X＝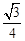
)；
(Ⅱ) 求数学期望E ( X )．
的前
项和
.
中，
，求数列
中，
，求数列
，其中
是自然常数，
时, 
的单调性、极值；
;
，使
（
）
相关知识点
推荐套卷
本题满分分已知A，B，C，D，E，F是边长为1的正六边形的6个顶点，在顶点取自A，B，C，D，E，F的所有三角形中，随机(等可能)取一个三角形．设随机变量X为取出三角形的面积．
(Ⅰ) 求概率P ( X＝)；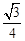
(Ⅱ) 求数学期望E ( X )．
粤公网安备 44130202000953号