如图，已知四棱锥S—ABCD中，△SAD是边长为a的正三角形，平面SAD⊥平面ABCD，四边形ABCD为菱形，∠DAB=60°，P为AD中点，Q为SB中点，（1）求证：PQ∥平面SCD；（2）求二面角B—PC—Q的正切值的大小。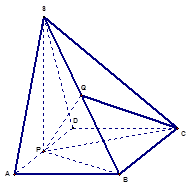
的方程为
，求直线
的方程，使得：（１）
；（２）
是
的边
上的点，且
．
与
互相平行，且
，
之间的距离为
，求直线
，点
，求证：
，且平行于直线
的直线方程是
；
．
，
到直线
的距离相等，求
的值．推荐套卷
如图，已知四棱锥S—ABCD中，△SAD是边长为a的正三角形，平面SAD⊥平面ABCD，四边形ABCD为菱形，∠DAB=60°，P为AD中点，Q为SB中点，（1）求证：PQ∥平面SCD；（2）求二面角B—PC—Q的正切值的大小。
粤公网安备 44130202000953号