（本小题满分15分）
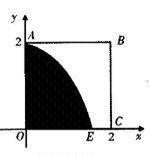
如图，某小区有一边长为2（单位：百米）的正方形地块OABC，其中OAE是一个游泳池，计划在地块OABC内修一条与池边AE相切的直路
（宽度不计），切点为M，并把该地块分为两部分．现以点O为坐标原点，以线段OC所在直线为x轴，建立平面直角坐标系，若池边AE满足函数
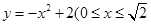）的图象，且点M到边OA距离为
．
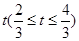（1）当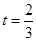
时，求直路所在的直线方程；
（2）当t为何值时，地块OABC在直路不含泳池那侧的面积取到最大，最大值是多少？
；
，求Sn；
，试证明：S1S2+S2S3+……+SnS
处的切线为
，若
相切，求a的值
的单调区间
，且
是
的中点．
∥平面
；
．
推荐套卷
（本小题满分15分）
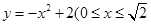如图，某小区有一边长为2（单位：百米）的正方形地块OABC，其中OAE是一个游泳池，计划在地块OABC内修一条与池边AE相切的直路（宽度不计），切点为M，并把该地块分为两部分．现以点O为坐标原点，以线段OC所在直线为x轴，建立平面直角坐标系，若池边AE满足函数）的图象，且点M到边OA距离为．
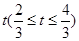（1）当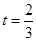时，求直路所在的直线方程；
（2）当t为何值时，地块OABC在直路不含泳池那侧的面积取到最大，最大值是多少？
粤公网安备 44130202000953号