（本小题满分15分）已知直线l的方程为：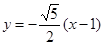
，直线l与x轴的交点为F， 圆O的方程为：
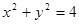，C、 D在圆上， CF⊥DF，设线段CD的中点为M．
（1）如果CFDG为平行四边形，求动点G的轨迹；
（2）已知椭圆的中心在原点，右焦点为F，直线l交椭圆于A、B两点，又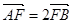
，
求椭圆C的方程．
相关试题
，
，
．
边上中线所在直线的方程（要求写成系数为整数的一般式方程）；
的面积
．
中，
，其中
．
项和
；
，使得
对任意
均成立
的各项均为正数,
,前
项和为
,
为等比数列,
,且
．
与
；
对任意正整数
恒成立，求实数
的取值范围．
的前n项和记为
．
的各项为正，其前
项和为
成等比数列，求
．
在内角
的对边分别为
,已知
．
；
，求△推荐套卷
（本小题满分15分）已知直线l的方程为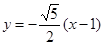：，直线l与x轴的交点为F， 圆O的方程为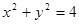：，C、 D在圆上， CF⊥DF，设线段CD的中点为M．
（1）如果CFDG为平行四边形，求动点G的轨迹；
（2）已知椭圆的中心在原点，右焦点为F，直线l交椭圆于A、B两点，又，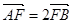
求椭圆C的方程．
粤公网安备 44130202000953号