(本小题12分)已知椭圆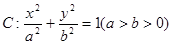 的离心率为
的离心率为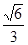 ,
,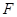 为椭圆的右焦点,
为椭圆的右焦点,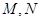 两点在椭圆
两点在椭圆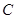 上,且
上,且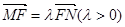 ,定点
,定点 。
。
(1)若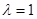 时,有
时,有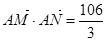 ,求椭圆
,求椭圆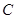 的方程;
的方程;
(2)在条件(1)所确定的椭圆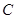 下,当动直线
下,当动直线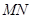 斜率为k,且设
斜率为k,且设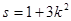 时,试求
时,试求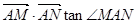 关于S的函数表达式f(s)的最大值,以及此时
关于S的函数表达式f(s)的最大值,以及此时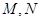 两点所在的直线方程。
两点所在的直线方程。
推荐套卷
(本小题12分)已知椭圆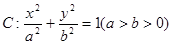 的离心率为
的离心率为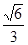 ,
,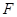 为椭圆的右焦点,
为椭圆的右焦点,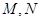 两点在椭圆
两点在椭圆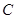 上,且
上,且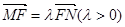 ,定点
,定点 。
。
(1)若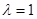 时,有
时,有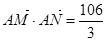 ,求椭圆
,求椭圆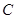 的方程;
的方程;
(2)在条件(1)所确定的椭圆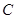 下,当动直线
下,当动直线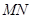 斜率为k,且设
斜率为k,且设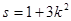 时,试求
时,试求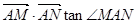 关于S的函数表达式f(s)的最大值,以及此时
关于S的函数表达式f(s)的最大值,以及此时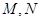 两点所在的直线方程。
两点所在的直线方程。