(本小题满分16分)已知函数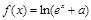 (
(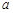 为常数)是实数集
为常数)是实数集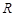 上的奇函数,函数
上的奇函数,函数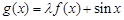 是区间
是区间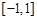 上的减函数。
上的减函数。
(1)求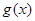 在
在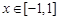 上的最大值;
上的最大值;
(2)若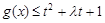 对
对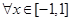 及
及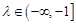 恒成立,求
恒成立,求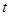 的取值范围;
的取值范围;
(3)讨论关于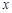 的方程
的方程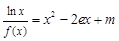 的根的个数。
的根的个数。
相关知识点
推荐套卷
(本小题满分16分)已知函数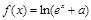 (
(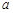 为常数)是实数集
为常数)是实数集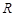 上的奇函数,函数
上的奇函数,函数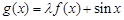 是区间
是区间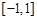 上的减函数。
上的减函数。
(1)求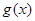 在
在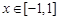 上的最大值;
上的最大值;
(2)若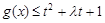 对
对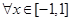 及
及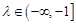 恒成立,求
恒成立,求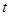 的取值范围;
的取值范围;
(3)讨论关于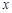 的方程
的方程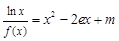 的根的个数。
的根的个数。