.(本小题满分14分)
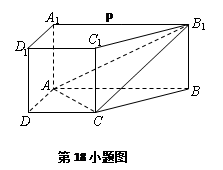
直棱柱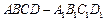 
中，底面 ABCD是直角梯形，∠ BAD＝∠ ADC＝90°， 
．
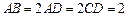(Ⅰ) 求证： AC⊥平面 BB 1 
C 1 C；
（Ⅱ）若P为 A 1 B 1的中点，求证： DP∥平面 BCB 1，且 DP∥平面 ACB 1．
的前
项和
．
，求数列
的前
中，
分别为
．
．
的对边，已知
，
，
．
的值．
即可,不必算出最结果.）
.
，求函数
的极值；
，且当
时，
12a恒成立，试确定
的取值范围.
在
中，a=
,b=6,A=
,解三角形推荐套卷
.(本小题满分14分)
直棱柱 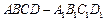中，底面 ABCD是直角梯形，∠ BAD＝∠ ADC＝90°， ．
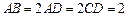(Ⅰ) 求证： AC⊥平面 BB 1 C 1 C；
（Ⅱ）若P为 A 1 B 1的中点，求证： DP∥平面 BCB 1，且 DP∥平面 ACB 1．
粤公网安备 44130202000953号