已知中心在原点的椭圆的一个焦点为（0 ，
），且过点
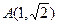，过A作倾斜角互补的两条直线，它们与椭圆的另一个交点分别为点B和点C。
（1）求椭圆的标准方程；
（2）求证：直线BC的斜率为定值，并求这个定值。
（3）求三角形ABC的面积最大值。
相关试题
中，
，
，
，设E为
的中点，F为
的中点，在给定的空间直角坐标系D－xyz下，试写出A，B，C，D，
，
，
，
，E，F各点的坐标．
平面内的直线
上确定一点
；使
的距离最小．
，
，0），点D在平面yoz上，且
BDC=900，
推荐套卷
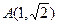已知中心在原点的椭圆的一个焦点为（0 ，），且过点，过A作倾斜角互补的两条直线，它们与椭圆的另一个交点分别为点B和点C。
（1）求椭圆的标准方程；
（2）求证：直线BC的斜率为定值，并求这个定值。
（3）求三角形ABC的面积最大值。
粤公网安备 44130202000953号