（本小题满分14分）
如图，在三棱锥P－ABC中，底面△ABC为等边三角形，∠APC＝90°，PB＝AC＝2PA＝4，O为AC的中点。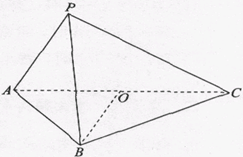
（Ⅰ）求证：BO⊥PA；
（Ⅱ）判断在线段AC上是否存在点Q（与点O不重合），使得△PQB为直角三角形？若存在，试找出一个点Q，并求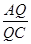
的值；若不存在，说明理由。
相关试题
中，
为
的中点，
分别在
上，且
,求
的值。
的值；
且
，
，求
的值。
，
与
夹角为
，求
与
夹角的余弦值。
，
，
.
时，若函数
在区间
上是单调增函数，试求
的取值范围；
时，直接写出（不需给出演算步骤）函数
（
）的单调增区间；
，使函数
，
（
）在
处取得最小值，试求实数
的最大值.推荐套卷
（本小题满分14分）
如图，在三棱锥P－ABC中，底面△ABC为等边三角形，∠APC＝90°，PB＝AC＝2PA＝4，O为AC的中点。
（Ⅰ）求证：BO⊥PA；
（Ⅱ）判断在线段AC上是否存在点Q（与点O不重合），使得△PQB为直角三角形？若存在，试找出一个点Q，并求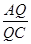的值；若不存在，说明理由。
粤公网安备 44130202000953号