(本小题满分14分)如图,已知直线OP1,OP2为双曲线E: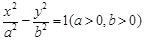 的渐近线,△P1OP2的面积为
的渐近线,△P1OP2的面积为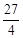 ,在双曲线E上存在点P为线段P1P2的一个三等分点,且双曲线E的离心率为
,在双曲线E上存在点P为线段P1P2的一个三等分点,且双曲线E的离心率为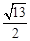 .
.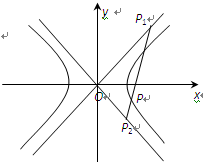
(1)若P1、P2点的横坐标分别为x1、x2,则x1、x2之间满足怎样的关系?并证明你的结论;
(2)求双曲线E的方程;
(3)设双曲线E上的动点 ,两焦点
,两焦点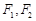 ,若
,若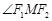 为钝角,求
为钝角,求 点横坐标
点横坐标 的取值范围.
的取值范围.
推荐套卷
(本小题满分14分)如图,已知直线OP1,OP2为双曲线E: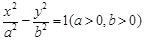 的渐近线,△P1OP2的面积为
的渐近线,△P1OP2的面积为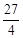 ,在双曲线E上存在点P为线段P1P2的一个三等分点,且双曲线E的离心率为
,在双曲线E上存在点P为线段P1P2的一个三等分点,且双曲线E的离心率为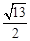 .
.
(1)若P1、P2点的横坐标分别为x1、x2,则x1、x2之间满足怎样的关系?并证明你的结论;
(2)求双曲线E的方程;
(3)设双曲线E上的动点 ,两焦点
,两焦点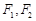 ,若
,若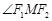 为钝角,求
为钝角,求 点横坐标
点横坐标 的取值范围.
的取值范围.