(本题13分)设椭圆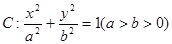 的左右焦点分别为
的左右焦点分别为 ,
,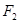 ,上顶点为
,上顶点为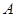 ,过点
,过点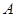 与
与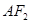 垂直的直线交
垂直的直线交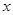 轴负半轴于
轴负半轴于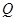 点,且
点,且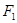 是
是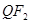 的中点.
的中点.
(1)求椭圆的离心率;
(2)若过点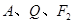 的圆恰好与直线
的圆恰好与直线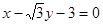 相切,求椭圆
相切,求椭圆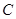 的方程;
的方程;
(3)在(2)的条件下过右焦点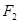 作斜率为
作斜率为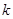 的直线
的直线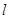 与椭圆相交于
与椭圆相交于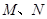 两点,在
两点,在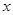 轴上是否存在点
轴上是否存在点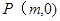 使得以
使得以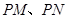 为邻边的平行四边形为菱形,如果存在,求出
为邻边的平行四边形为菱形,如果存在,求出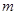 的取值范围,如果不存在,说明理由。
的取值范围,如果不存在,说明理由。
推荐套卷
(本题13分)设椭圆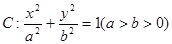 的左右焦点分别为
的左右焦点分别为 ,
,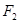 ,上顶点为
,上顶点为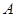 ,过点
,过点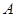 与
与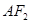 垂直的直线交
垂直的直线交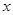 轴负半轴于
轴负半轴于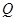 点,且
点,且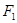 是
是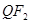 的中点.
的中点.
(1)求椭圆的离心率;
(2)若过点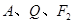 的圆恰好与直线
的圆恰好与直线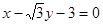 相切,求椭圆
相切,求椭圆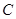 的方程;
的方程;
(3)在(2)的条件下过右焦点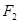 作斜率为
作斜率为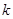 的直线
的直线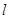 与椭圆相交于
与椭圆相交于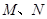 两点,在
两点,在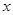 轴上是否存在点
轴上是否存在点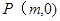 使得以
使得以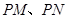 为邻边的平行四边形为菱形,如果存在,求出
为邻边的平行四边形为菱形,如果存在,求出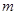 的取值范围,如果不存在,说明理由。
的取值范围,如果不存在,说明理由。