(A、B选做一题,若两题都做,以A题计分,本题满分14分)
A.已知向量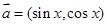 ,
, ,
,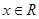 ,函数
,函数
(1)求函数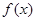 的最大值与最小正周期;
的最大值与最小正周期;
(2)求使不等式 成立的
成立的 的取值集合.
的取值集合.
(3)若将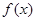 向左平移
向左平移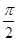 个单位,再把图象所有点的横坐标缩短到原来的
个单位,再把图象所有点的横坐标缩短到原来的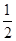 倍得到
倍得到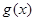 ,关于
,关于 的方程
的方程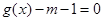 在
在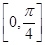 有且仅有一个解,求
有且仅有一个解,求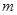 的取值范围。
的取值范围。
推荐套卷
(A、B选做一题,若两题都做,以A题计分,本题满分14分)
A.已知向量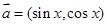 ,
, ,
,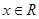 ,函数
,函数
(1)求函数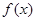 的最大值与最小正周期;
的最大值与最小正周期;
(2)求使不等式 成立的
成立的 的取值集合.
的取值集合.
(3)若将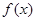 向左平移
向左平移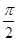 个单位,再把图象所有点的横坐标缩短到原来的
个单位,再把图象所有点的横坐标缩短到原来的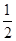 倍得到
倍得到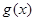 ,关于
,关于 的方程
的方程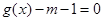 在
在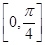 有且仅有一个解,求
有且仅有一个解,求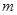 的取值范围。
的取值范围。