（本小题满分12分） 已知直线L：y=x+1与曲线C：
交于不同的两点A,B;O为坐标原点。
（1）若
，试探究在曲线C上仅存在几个点到直线L的距离恰为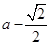
？并说明理由；
（2）若
，且a>b,
,试求曲线C的离心率e的取值范围。
相关试题
。
，求函数
的值；
，函数f(x)＝
，x∈[0，π]。
与
夹角的大小。
，
，
与
的夹角为
。求：
；
； 
中，
，求
均为锐角，求
的值。
为平面的一组基向量，
,
,
与
交与点
关于
，
,求
;
交直线
于
两点，设
，
）求
的关系式。
推荐套卷
（本小题满分12分） 已知直线L：y=x+1与曲线C：交于不同的两点A,B;O为坐标原点。
（1）若，试探究在曲线C上仅存在几个点到直线L的距离恰为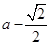？并说明理由；
（2）若，且a>b,,试求曲线C的离心率e的取值范围。
粤公网安备 44130202000953号