（本小题满分12分）
已知椭圆C :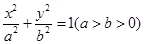
经过点
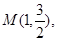离心率为
。
（Ⅰ） 求椭圆C的方程；
（Ⅱ）设直线l与椭圆C相交于A、B两点，以线段OA、OB为邻边作平行四边形OAPB，其中顶点P在椭圆C上，O为坐标原点。求O到直线l的距离的最小值。
相关试题
中，
．
是等比数列，并求
；
满足
，数列
，
对一切
恒成立，求
的取值范围．
分别为∠A、∠B、∠C所对的边，且
，求△ABC周长的取值范围．
的前四项的和为
，且
成等比数列．
与前n项和
；
为数列
的前n项和，求
实数
满足
，命题
实数
，若
是
的充分不必要条件，求实数
的取值范围．
的不等式
的解集为
．
的值；
（
为常数）．推荐套卷
（本小题满分12分）
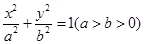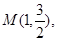已知椭圆C :经过点离心率为。
（Ⅰ） 求椭圆C的方程；
（Ⅱ）设直线l与椭圆C相交于A、B两点，以线段OA、OB为邻边作平行四边形OAPB，其中顶点P在椭圆C上，O为坐标原点。求O到直线l的距离的最小值。
粤公网安备 44130202000953号